| |
There were five stop watches on the table,
as shown in the figure here, of same make, design and size. I deduced
that the difference had to be elsewhere and pondered over the solution
of the problem for a while. The watches had only the hours’ hands that
pointed at 1, 4, 6, 8 and 9, respectively. For a while, I thought that
these numbers were in series, but it was not so. There were two odd
numbers and three even ones, so, none could be singled out. "Time
up!" said the professor, "You failed to notice that only the
first watch pointed at a number that was prime. A prime number is
divisible only by 1 and itself."
 Realising my
disappointment, he decided to give me another chance and asked me if I
would like to solve one more problem. After I accepted the challenge, he
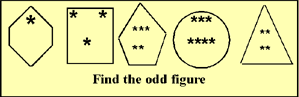
said, "I have five star charts — a hexagon with one star, a
rectangle with three stars, a pentagon with five stars, a circle with
seven stars and a triangle with four stars — and you have to pick the
odd one out of these." The circle, as shown in the second figure
here, looked odd to me, but the professor said it was not the one. After
much thought, I said, "It looks to be an out of the world
problem." "You presume correctly. These charts show position
of stars that are out of this world, unlike Jackie Chan," said the
professor. "Observe that the number of stars and angles (or sides)
in all figures, except the pentagon, add up to seven," he said.
"Look at the figures now, what do you see?" "Stars,"
I said. "Stars! What stars? Wake up silly," I heard my father
say, "it is 11.30 now, don’t you have to attend Narlikar’s
lecture?" I realised that it had indeed been a dream encounter with
my star. Realising my
disappointment, he decided to give me another chance and asked me if I
would like to solve one more problem. After I accepted the challenge, he
said, "I have five star charts — a hexagon with one star, a
rectangle with three stars, a pentagon with five stars, a circle with
seven stars and a triangle with four stars — and you have to pick the
odd one out of these." The circle, as shown in the second figure
here, looked odd to me, but the professor said it was not the one. After
much thought, I said, "It looks to be an out of the world
problem." "You presume correctly. These charts show position
of stars that are out of this world, unlike Jackie Chan," said the
professor. "Observe that the number of stars and angles (or sides)
in all figures, except the pentagon, add up to seven," he said.
"Look at the figures now, what do you see?" "Stars,"
I said. "Stars! What stars? Wake up silly," I heard my father
say, "it is 11.30 now, don’t you have to attend Narlikar’s
lecture?" I realised that it had indeed been a dream encounter with
my star.
— Aditya Rishi
|

